Fits a phylogenetic structural equation model
Usage
phylosem(
sem,
tree,
data,
family = rep("fixed", ncol(data)),
covs = colnames(data),
estimate_ou = FALSE,
estimate_lambda = FALSE,
estimate_kappa = FALSE,
data_labels = rownames(data),
tmb_inputs = NULL,
control = phylosem_control()
)Arguments
- sem
structural equation model structure, passed to either
specifyModelorspecifyEquationsand then parsed to control the set of path coefficients and variance-covariance parameters- tree
phylogenetic structure, using class
as.phylo- data
data-frame providing variables being modeled. Missing values are inputted as NA. If an SEM includes a latent variable (i.e., variable with no available measurements) then it still must be inputted as a column of
datawith entirely NA values.- family
Character-vector listing the distribution used for each column of
data, where each element must befixed,normal,binomial, orpoisson.family="fixed"is default behavior and assumes that a given variable is measured exactly. Other options correspond to different specifications of measurement error.- covs
optional: a character vector of one or more elements, with each element giving a string of variable names, separated by commas. Variances and covariances among all variables in each such string are added to the model. For confirmatory factor analysis models specified via
cfa,covsdefaults to all of the factors in the model, thus specifying all variances and covariances among these factors. Warning:covs="x1, x2"andcovs=c("x1", "x2")are not equivalent:covs="x1, x2"specifies the variance ofx1, the variance ofx2, and their covariance, whilecovs=c("x1", "x2")specifies the variance ofx1and the variance ofx2but not their covariance.- estimate_ou
Boolean indicating whether to estimate an autoregressive (Ornstein-Uhlenbeck) process using additional parameter
lnalpha, corresponding to themodel="OUrandomRoot"parameterization from phylolm as listed in doi:10.1093/sysbio/syu005- estimate_lambda
Boolean indicating whether to estimate additional branch lengths for phylogenetic tips (a.k.a. the Pagel-lambda term) using additional parameter
logitlambda- estimate_kappa
Boolean indicating whether to estimate a nonlinear scaling of branch lengths (a.k.a. the Pagel-kappa term) using additional parameter
lnkappa- data_labels
For each row of
data, listing the corresponding name fromtree$tip.label. Default pullsdata_labelsfromrownames(data)- tmb_inputs
optional tagged list that overrides the default constructor for TMB inputs (use at your own risk)
- control
Output from
phylosem_control, used to define user settings, and see documentation for that function for details.
Value
An object (list) of class `phylosem`. Elements include:
- data
Copy of argument
data- SEM_model
SEM model parsed from
semusingspecifyModelorspecifyEquations- obj
TMB object from
MakeADFun- tree
Copy of argument
tree- tmb_inputs
The list of inputs passed to
MakeADFun- opt
The output from
nlminb- sdrep
The output from
sdreport- report
The output from
obj$report()- parhat
The output from
obj$env$parList()containing maximum likelihood estimates and empirical Bayes predictions
Details
Note that parameters logitlambda, lnkappa, and lnalpha if estimated are each estimated as having a single value
that applies to all modeled variables.
This differs from default behavior in phylolm, where these parameters only apply to the "response" and not "predictor" variables.
This also differs from default behavior in phylopath, where a different value is estimated
in each call to phylolm during the d-separation estimate of path coefficients. However, it is
consistent with default behavior in Rphylopars, and estimates should be comparable in that case.
These additional parameters are estimated with unbounded support, which differs somewhat from default
bounded estimates in phylolm, although parameters should match if overriding phylolm defaults
to use unbounded support. Finally, phylosem allows these three parameters to be estimated in any
combination, which is expanded functionality relative to the single-option functionality in phylolm.
Also note that phylopath by default uses standardized coefficients. To achieve matching parameter estimates between phylosem and phylopath, standardize each variable to have a standard deviation of 1.0 prior to fitting with phylosem.
References
**Introducing the package, its features, and comparison with other software (to cite when using phylosem):**
Thorson, J. T., & van der Bijl, W. (In press). phylosem: A fast and simple R package for phylogenetic inference and trait imputation using phylogenetic structural equation models. Journal of Evolutionary Biology. doi:10.1111/jeb.14234
*Statistical methods for phylogenetic structural equation models*
Thorson, J. T., Maureaud, A. A., Frelat, R., Merigot, B., Bigman, J. S., Friedman, S. T., Palomares, M. L. D., Pinsky, M. L., Price, S. A., & Wainwright, P. (2023). Identifying direct and indirect associations among traits by merging phylogenetic comparative methods and structural equation models. Methods in Ecology and Evolution, 14(5), 1259-1275. doi:10.1111/2041-210X.14076
*Earlier development of computational methods, originally used for phlogenetic factor analysis:*
Thorson, J. T. (2020). Predicting recruitment density dependence and intrinsic growth rate for all fishes worldwide using a data-integrated life-history model. Fish and Fisheries, 21(2), 237-251. doi:10.1111/faf.12427
Thorson, J. T., Munch, S. B., Cope, J. M., & Gao, J. (2017). Predicting life history parameters for all fishes worldwide. Ecological Applications, 27(8), 2262-2276. doi:10.1002/eap.1606
*Earlier development of phylogenetic path analysis:*
van der Bijl, W. (2018). phylopath: Easy phylogenetic path analysis in R. PeerJ, 6, e4718. doi:10.7717/peerj.4718
von Hardenberg, A., & Gonzalez-Voyer, A. (2013). Disentangling evolutionary cause-effect relationships with phylogenetic confirmatory path analysis. Evolution; International Journal of Organic Evolution, 67(2), 378-387. doi:10.1111/j.1558-5646.2012.01790.x
*Interface involving SEM `arrow notation` is repurposed from:*
Fox, J., Nie, Z., & Byrnes, J. (2020). Sem: Structural equation models. R package version 3.1-11. https://CRAN.R-project.org/package=sem
*Coercing output to phylo4d depends upon:*
Bolker, B., Butler, M., Cowan, P., de Vienne, D., Eddelbuettel, D., Holder, M., Jombart, T., Kembel, S., Michonneau, F., & Orme, B. (2015). phylobase: Base package for phylogenetic structures and comparative data. R Package Version 0.8.0. https://CRAN.R-project.org/package=phylobase
*Laplace approximation for parameter estimation depends upon:*
Kristensen, K., Nielsen, A., Berg, C. W., Skaug, H., & Bell, B. M. (2016). TMB: Automatic differentiation and Laplace approximation. Journal of Statistical Software, 70(5), 1-21. doi:10.18637/jss.v070.i05
Examples
# Load data set
data(rhino, rhino_tree, package="phylopath")
# Run phylosem
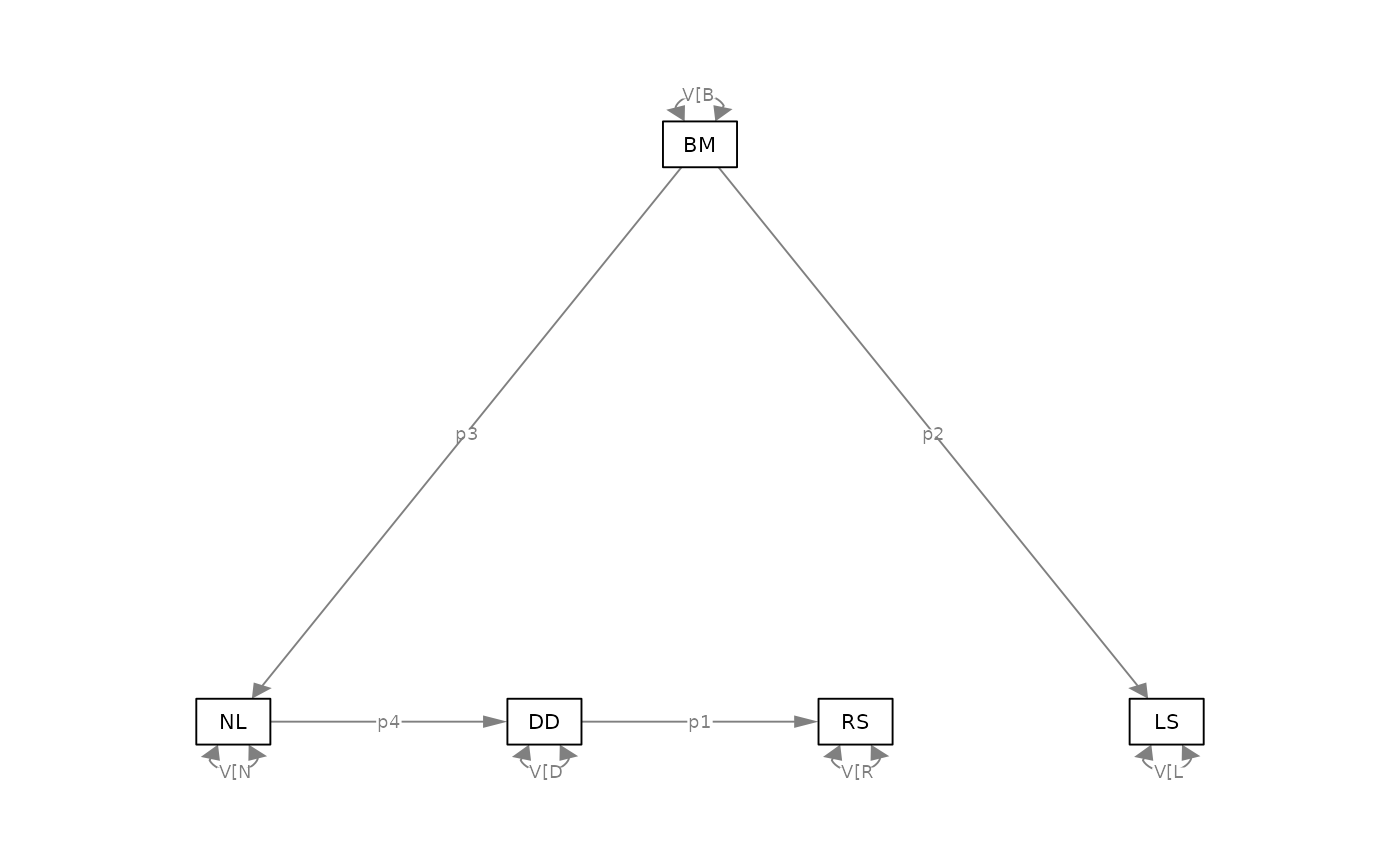
model = "
DD -> RS, p1
BM -> LS, p2
BM -> NL, p3
NL -> DD, p4
"
psem = phylosem( sem = model,
data = rhino[,c("BM","NL","DD","RS","LS")],
tree = rhino_tree )
#> NOTE: it is generally simpler to use specifyEquations() or cfa()
#> see ?specifyEquations
#> List of estimated fixed and random effects:
#> Coefficient_name Number_of_coefficients Type
#> 1 beta_z 9 Fixed
#> 2 x_vj 495 Random
#> Running nlminb_loop #1
#> Running newton_loop #1
#> Running sdreport
# Convert and plot using phylopath
library(phylopath)
#>
#> Attaching package: ‘phylopath’
#> The following objects are masked from ‘package:phylosem’:
#>
#> average, best, choice
my_fitted_DAG = as_fitted_DAG(psem)
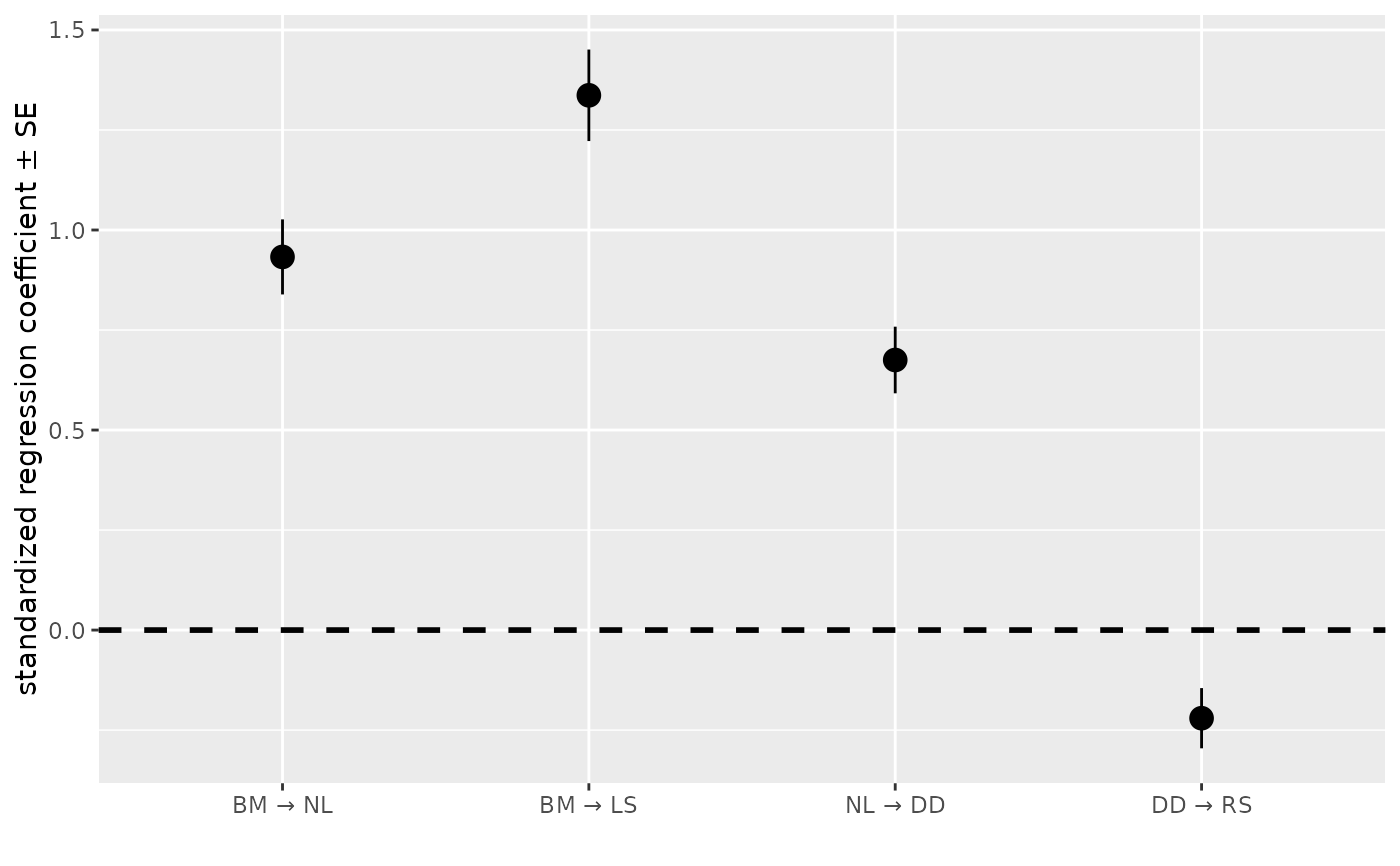
coef_plot( my_fitted_DAG )
#> The fitted model does not contain confidence intervals, so showing standard errors instead. Fit the model with `boot` larger than 0 to get confidence intervals, or set `error_bar = "se"` to avoid this warning.
plot( my_fitted_DAG )
# Convert to phylo4d to extract estimated traits and Standard errors
# for all ancestors and tips in the tree.
# In this rhino example, note that species are labeled s1-s100
# and ancestral nodes are not named.
(traits_est = as_phylo4d(psem))
#> label node ancestor edge.length node.type BM NL
#> 1 s1 1 107 0.5640308162 tip -0.76690456 -2.01757398
#> 2 s2 2 107 0.5640308162 tip -1.00970438 -1.74246592
#> 3 s3 3 106 0.6358275951 tip -1.22528123 -2.46855326
#> 4 s4 4 105 0.7144448083 tip 1.33053521 0.34055901
#> 5 s5 5 104 1.1830950600 tip 2.49234369 1.22400475
#> 6 s6 6 109 0.0361022107 tip 1.42514860 2.96922655
#> 7 s7 7 109 0.0361022107 tip 0.35610742 2.01122280
#> 8 s8 8 112 0.5022074646 tip -0.53161422 0.18490174
#> 9 s9 9 112 0.5022074646 tip -0.15373314 0.81809201
#> 10 s10 10 111 1.7871837580 tip 1.11171876 1.24302184
#> 11 s11 11 116 0.5913975424 tip 0.19579448 2.13282693
#> 12 s12 12 119 0.0477228892 tip 0.20125048 3.08972748
#> 13 s13 13 119 0.0477228892 tip 1.52219709 2.96228199
#> 14 s14 14 120 0.1142573039 tip -1.00338251 1.86652322
#> 15 s15 15 120 0.1142573039 tip 1.07689653 1.52906374
#> 16 s16 16 121 0.2756963162 tip 1.61531748 3.57241266
#> 17 s17 17 121 0.2756963162 tip -0.17420285 0.43146654
#> 18 s18 18 122 0.5512595516 tip 2.90711896 3.25268633
#> 19 s19 19 123 0.0349638989 tip 2.40453010 2.24981247
#> 20 s20 20 123 0.0349638989 tip 0.82895203 1.20324781
#> 21 s21 21 114 0.8767527377 tip 2.64255460 3.86427495
#> 22 s22 22 113 1.7461743450 tip -0.07719953 3.19026617
#> 23 s23 23 125 0.9075157185 tip -0.30484408 3.51060091
#> 24 s24 24 125 0.9075157185 tip 1.52258759 3.21435348
#> 25 s25 25 126 0.5415591015 tip 1.23860573 2.04363009
#> 26 s26 26 127 0.1089356405 tip 1.95343200 3.06738965
#> 27 s27 27 127 0.1089356405 tip 1.68648719 4.22039397
#> 28 s28 28 130 3.0857795440 tip 1.23934345 2.26507981
#> 29 s29 29 131 1.6399242000 tip -1.10263719 -1.63892351
#> 30 s30 30 132 0.8944032869 tip 0.08301170 0.42665712
#> 31 s31 31 133 0.7715950937 tip 1.01879042 0.03819250
#> 32 s32 32 133 0.7715950937 tip 0.02167732 -0.37157709
#> 33 s33 33 136 0.8699913472 tip 0.73065935 1.95289384
#> 34 s34 34 137 0.8479589114 tip 2.72407349 3.49784027
#> 35 s35 35 137 0.8479589114 tip 3.76646555 4.49878875
#> 36 s36 36 138 0.4591954289 tip -2.33729326 1.74995773
#> 37 s37 37 139 0.1736071099 tip 0.30205947 2.68777644
#> 38 s38 38 139 0.1736071099 tip -1.33960415 1.76434408
#> 39 s39 39 141 2.0905969730 tip 4.27686830 3.21806190
#> 40 s40 40 143 0.0744131178 tip 1.25068016 -0.71254314
#> 41 s41 41 143 0.0744131178 tip 1.41155371 -0.43526905
#> 42 s42 42 144 0.9370864528 tip 0.08393879 0.23591102
#> 43 s43 43 145 0.0881684468 tip 2.84964114 0.68816551
#> 44 s44 44 145 0.0881684468 tip 2.99095373 1.80145127
#> 45 s45 45 147 1.7204295900 tip 5.13749665 4.26473497
#> 46 s46 46 149 1.1842473100 tip 2.58859925 1.56946821
#> 47 s47 47 149 1.1842473100 tip 1.43384898 1.65242204
#> 48 s48 48 150 1.0253154590 tip 2.80876268 3.24344386
#> 49 s49 49 152 0.7195368746 tip 1.22593514 5.02896634
#> 50 s50 50 152 0.7195368746 tip 2.61927222 0.67351377
#> 51 s51 51 153 0.3613256451 tip 2.30223945 1.34901806
#> 52 s52 52 153 0.3613256451 tip 2.56528288 1.45099218
#> 53 s53 53 155 0.3002640020 tip 0.40340933 -1.65526609
#> 54 s54 54 155 0.3002640020 tip 0.88479865 -1.98334601
#> 55 s55 55 154 0.5937157619 tip 0.46893874 -0.62261098
#> 56 s56 56 156 3.2486997580 tip 2.95039314 4.03454344
#> 57 s57 57 161 0.4215356986 tip 1.53656023 0.46891422
#> 58 s58 58 161 0.4215356986 tip 2.50142020 0.45568152
#> 59 s59 59 162 0.0698869058 tip 2.33417280 -0.61028405
#> 60 s60 60 162 0.0698869058 tip 2.39854268 0.90424064
#> 61 s61 61 164 0.9090035873 tip 1.15944783 0.14368777
#> 62 s62 62 165 0.7237639845 tip 0.59250982 -1.00793024
#> 63 s63 63 167 0.3390345394 tip -0.70393275 -1.59874559
#> 64 s64 64 167 0.3390345394 tip 1.58394613 0.45296021
#> 65 s65 65 168 0.3269574705 tip 1.59263345 0.56850859
#> 66 s66 66 168 0.3269574705 tip 2.15658024 -0.88396728
#> 67 s67 67 170 0.4816150364 tip 5.26743199 2.18963416
#> 68 s68 68 171 0.0359279485 tip 1.34622701 -1.84421537
#> 69 s69 69 171 0.0359279485 tip 2.18241698 -0.76580964
#> 70 s70 70 173 0.6413136611 tip 2.93983039 -0.11351013
#> 71 s71 71 175 0.0945133814 tip 3.01129396 1.25866166
#> 72 s72 72 176 0.0006422211 tip 2.59398228 1.21303645
#> 73 s73 73 176 0.0006422211 tip 2.71938915 1.62942984
#> 74 s74 74 174 0.3139612126 tip 2.60745101 0.91920273
#> 75 s75 75 177 0.0359670563 tip 4.86547665 0.44478185
#> 76 s76 76 177 0.0359670563 tip 5.43684487 0.22107243
#> 77 s77 77 180 0.8668137583 tip 1.58687164 1.50654438
#> 78 s78 78 181 0.5981367654 tip 0.09365673 0.40527336
#> 79 s79 79 182 0.0727809267 tip 0.27286020 0.21689207
#> 80 s80 80 182 0.0727809267 tip 2.25220200 -1.07873909
#> 81 s81 81 179 1.5434906440 tip 1.05736541 -0.05289912
#> 82 s82 82 183 0.8078943991 tip 4.69785604 0.33163484
#> 83 s83 83 184 0.4661635151 tip 3.52231773 1.69620670
#> 84 s84 84 185 0.1900157199 tip 1.60779377 2.53614523
#> 85 s85 85 185 0.1900157199 tip 1.90789841 2.74261353
#> 86 s86 86 188 0.2378751898 tip 3.94393984 -1.28344814
#> 87 s87 87 190 0.0040209131 tip 2.67507049 -0.72928762
#> 88 s88 88 190 0.0040209131 tip 4.02248087 1.27038228
#> 89 s89 89 189 0.0295310172 tip 4.11611390 0.89924275
#> 90 s90 90 195 0.3502461608 tip 2.45594624 0.51529773
#> 91 s91 91 196 0.1859710332 tip 4.14053815 2.17333172
#> 92 s92 92 196 0.1859710332 tip 3.16070940 -0.62189645
#> 93 s93 93 194 0.8106943515 tip 2.97788577 -0.22596947
#> 94 s94 94 193 0.8259283637 tip 3.93086602 1.00077297
#> 95 s95 95 197 0.4469879611 tip 1.54045681 0.11089573
#> 96 s96 96 197 0.4469879611 tip 1.04974779 2.05813396
#> 97 s97 97 198 0.2644025504 tip 4.08564283 1.22297875
#> 98 s98 98 198 0.2644025504 tip 3.47019109 1.80421473
#> 99 s99 99 199 0.0717127012 tip -1.51698326 -2.66773226
#> 100 s100 100 199 0.0717127012 tip -1.55493000 -1.25446488
#> 101 <NA> 101 0 NA root 1.37537396 1.29911665
#> 102 <NA> 102 101 0.3278789676 internal 1.16700652 1.46268576
#> 103 <NA> 103 102 0.0448143702 internal 1.14127151 1.44843940
#> 104 <NA> 104 103 1.7536273230 internal 0.80116123 -0.04630783
#> 105 <NA> 105 104 0.4686502517 internal 0.04035308 -0.94897241
#> 106 <NA> 106 105 0.0786172132 internal -0.22924544 -1.24229608
#> 107 <NA> 107 106 0.0717967789 internal -0.36298395 -1.37170519
#> 108 <NA> 108 103 0.5388417629 internal 0.93634388 1.73643821
#> 109 <NA> 109 108 2.3617784090 internal 0.89097477 2.48450717
#> 110 <NA> 110 108 0.1838847379 internal 0.86994281 1.77647687
#> 111 <NA> 111 110 0.4268121240 internal 0.68585957 1.45889941
#> 112 <NA> 112 111 1.2849762930 internal -0.17453886 0.65800392
#> 113 <NA> 113 110 0.4678215366 internal 0.90278222 2.22643059
#> 114 <NA> 114 113 0.8694216075 internal 1.45174623 2.58275128
#> 115 <NA> 115 114 0.0071530214 internal 1.44654748 2.57522749
#> 116 <NA> 116 115 0.2782021739 internal 0.86447464 2.32881108
#> 117 <NA> 117 116 0.1696001798 internal 0.70138920 2.23479250
#> 118 <NA> 118 117 0.1745800373 internal 0.52173009 2.28117789
#> 119 <NA> 119 118 0.1994944362 internal 0.82540175 2.94643376
#> 120 <NA> 120 118 0.1329600215 internal 0.18250929 1.87312200
#> 121 <NA> 121 117 0.1461010464 internal 0.71125182 2.11498215
#> 122 <NA> 122 115 0.3183401648 internal 1.88123312 2.52235493
#> 123 <NA> 123 122 0.5162956527 internal 1.62540354 1.75259450
#> 124 <NA> 124 102 1.5076279270 internal 1.07467482 2.69406705
#> 125 <NA> 125 124 0.5663931071 internal 0.81605854 3.06517183
#> 126 <NA> 126 124 0.9323497240 internal 1.44328773 2.84469772
#> 127 <NA> 127 126 0.4326234610 internal 1.77783916 3.55452384
#> 128 <NA> 128 101 0.0206999989 internal 1.38852884 1.28879004
#> 129 <NA> 129 128 0.2000464880 internal 1.33869173 1.25256763
#> 130 <NA> 130 129 0.0028896898 internal 1.33645716 1.25093770
#> 131 <NA> 131 130 1.4458553430 internal 0.26389060 -0.03977885
#> 132 <NA> 132 131 0.7455209135 internal 0.33208018 0.02167613
#> 133 <NA> 133 132 0.1228081933 internal 0.37751187 -0.02380741
#> 134 <NA> 134 129 0.6949407786 internal 1.70295554 1.51871663
#> 135 <NA> 135 134 0.9138552433 internal 1.13478525 2.30724483
#> 136 <NA> 136 135 0.6098818644 internal 1.98297090 2.97989486
#> 137 <NA> 137 136 0.0220324358 internal 2.04532689 3.03020353
#> 138 <NA> 138 135 1.0206777830 internal -0.91929472 2.06222134
#> 139 <NA> 139 138 0.2855883190 internal -0.61213304 2.18786984
#> 140 <NA> 140 134 0.0802496379 internal 1.79491314 1.48020658
#> 141 <NA> 141 140 0.2228818440 internal 1.93611785 1.40251215
#> 142 <NA> 142 141 0.2076500851 internal 1.83517586 1.14979654
#> 143 <NA> 143 142 1.8085337700 internal 1.34127779 -0.53915958
#> 144 <NA> 144 142 0.9458604351 internal 1.63368609 0.88198103
#> 145 <NA> 145 144 0.8489180060 internal 2.85678218 1.22689695
#> 146 <NA> 146 140 0.1770607381 internal 1.88563084 1.45696065
#> 147 <NA> 147 146 0.4159884892 internal 2.40357460 2.04245093
#> 148 <NA> 148 147 0.1695261804 internal 2.34525741 2.06207604
#> 149 <NA> 149 148 0.3666560998 internal 2.21751655 1.88955477
#> 150 <NA> 150 148 0.5255879506 internal 2.34756636 2.37022333
#> 151 <NA> 151 150 0.2079515725 internal 2.25494138 2.31503928
#> 152 <NA> 152 151 0.0978270115 internal 2.18389259 2.42967093
#> 153 <NA> 153 151 0.4560382411 internal 2.38302136 1.65964448
#> 154 <NA> 154 146 1.5427023170 internal 0.75523426 -0.91688085
#> 155 <NA> 155 154 0.2934517599 internal 0.68171630 -1.51387805
#> 156 <NA> 156 128 0.0400159638 internal 1.42392811 1.27607295
#> 157 <NA> 157 156 0.4026925133 internal 1.59094851 0.80617095
#> 158 <NA> 158 157 0.7951233038 internal 1.94014906 0.57576258
#> 159 <NA> 159 158 0.3736798197 internal 2.09528413 0.38387613
#> 160 <NA> 160 159 1.1492712710 internal 2.14639670 0.34532781
#> 161 <NA> 161 160 0.1063971509 internal 2.10365653 0.38456695
#> 162 <NA> 162 160 0.4580459438 internal 2.35076674 0.16103746
#> 163 <NA> 163 159 0.2335971502 internal 2.18187420 0.27175804
#> 164 <NA> 164 163 0.5346033834 internal 1.43309091 -0.13103237
#> 165 <NA> 165 164 0.1852396028 internal 1.22940201 -0.32658223
#> 166 <NA> 166 165 0.1474062575 internal 1.19702794 -0.34342541
#> 167 <NA> 167 166 0.2373231876 internal 0.75543298 -0.47728109
#> 168 <NA> 168 166 0.2494002564 internal 1.60632063 -0.23125539
#> 169 <NA> 169 163 0.4262080943 internal 2.93682275 0.38831503
#> 170 <NA> 170 169 0.5357838400 internal 3.31558918 0.40274303
#> 171 <NA> 171 170 0.4456870879 internal 1.82442522 -1.23884620
#> 172 <NA> 172 169 0.3680846598 internal 3.32860306 0.47906468
#> 173 <NA> 173 172 0.0080005555 internal 3.31402225 0.48288912
#> 174 <NA> 174 173 0.3273524485 internal 2.90843309 0.94379679
#> 175 <NA> 175 174 0.2194478311 internal 2.84691345 1.26996664
#> 176 <NA> 176 175 0.0938711603 internal 2.65733422 1.42071746
#> 177 <NA> 177 172 0.6133471602 internal 5.09924499 0.33708989
#> 178 <NA> 178 158 0.3661103260 internal 1.94894404 0.65767175
#> 179 <NA> 179 178 0.1412829703 internal 1.78053559 0.59541556
#> 180 <NA> 180 179 0.6766768859 internal 1.29098355 0.58146426
#> 181 <NA> 181 180 0.2686769929 internal 1.00489189 0.28918765
#> 182 <NA> 182 181 0.5253558386 internal 1.24584098 -0.38427402
#> 183 <NA> 183 178 0.8768792154 internal 3.01524389 1.24025010
#> 184 <NA> 184 183 0.3417308840 internal 2.71906704 1.85162298
#> 185 <NA> 185 184 0.2761477952 internal 2.00389796 2.43773069
#> 186 <NA> 186 157 0.4967710625 internal 1.57881801 0.37044145
#> 187 <NA> 187 186 0.8026320886 internal 2.63989652 0.47536690
#> 188 <NA> 188 187 1.3087289040 internal 3.73176237 -0.25942644
#> 189 <NA> 189 188 0.2083441725 internal 3.71974615 0.52049204
#> 190 <NA> 190 189 0.0255101041 internal 3.37587615 0.28880652
#> 191 <NA> 191 187 0.3703056422 internal 2.82049596 0.73168597
#> 192 <NA> 192 191 0.1968950188 internal 2.73597270 0.72052113
#> 193 <NA> 193 192 0.1534750686 internal 2.96263400 0.63791542
#> 194 <NA> 194 193 0.0152340122 internal 2.96727375 0.62302314
#> 195 <NA> 195 194 0.4604481907 internal 3.10148300 0.65510394
#> 196 <NA> 196 195 0.1642751276 internal 3.45213971 0.73212244
#> 197 <NA> 197 192 0.5324154713 internal 1.72111346 0.97689560
#> 198 <NA> 198 191 0.9118959007 internal 3.65669043 1.41459293
#> 199 <NA> 199 186 2.2775234810 internal -1.48767902 -1.92496075
#> DD RS LS
#> 1 -0.792261887 -3.392696532 -0.094767133
#> 2 1.764320772 -1.046718911 -2.146334945
#> 3 -1.806155037 -2.859660611 -0.632068429
#> 4 0.948874128 -0.278689412 -0.134264890
#> 5 1.624151256 0.220814157 0.608236202
#> 6 2.252422051 2.426804694 3.085533985
#> 7 4.108146451 1.633655726 1.223147978
#> 8 -1.160995541 0.999431600 0.517537813
#> 9 1.341758025 1.304985166 1.521502859
#> 10 0.570073147 0.720705268 1.017846421
#> 11 2.828030732 2.001705516 -0.919563025
#> 12 2.980595831 1.521314671 0.131015359
#> 13 1.359162717 2.162885763 1.163026706
#> 14 1.848692884 1.583433981 0.927126010
#> 15 2.141254323 0.189198068 1.812639133
#> 16 1.560178083 2.781747914 3.347392203
#> 17 -0.073939690 0.027354662 0.900742360
#> 18 3.402771712 -0.457261541 -0.106852864
#> 19 2.876235296 0.463291813 1.744751921
#> 20 2.660581053 0.222790773 -0.532153665
#> 21 2.299374032 3.217700305 -1.138669460
#> 22 1.993843377 2.765155326 -0.621091021
#> 23 2.443433385 2.335835676 0.469978073
#> 24 3.979027350 3.226436578 2.780465714
#> 25 2.034137013 0.942969691 3.576663764
#> 26 3.027626293 1.238032443 3.065084710
#> 27 3.714825776 1.176979136 1.534261968
#> 28 0.675597786 2.317952086 -0.218626950
#> 29 -2.974709277 -1.760554760 -1.239583231
#> 30 0.867846728 2.592129904 0.021198341
#> 31 -1.320245499 0.237320570 -0.105135494
#> 32 -1.143376610 0.425657695 0.271740269
#> 33 3.123728954 1.116995185 3.162476646
#> 34 1.753272053 2.688262363 4.250866454
#> 35 1.210588042 1.223837757 2.943572655
#> 36 0.909660193 2.451038343 1.895478114
#> 37 1.859861867 0.828466484 2.481719676
#> 38 2.717730773 0.796806294 1.126178674
#> 39 4.477326061 2.610442179 1.465738306
#> 40 2.277574874 0.484494584 1.791592125
#> 41 1.593822132 1.454823177 0.729183055
#> 42 2.322463839 0.204364321 -0.885061737
#> 43 2.292615149 -1.418461690 3.138543805
#> 44 2.146223656 -0.184209303 3.099199564
#> 45 2.055324236 2.083887955 2.952789127
#> 46 2.486684424 1.457198741 4.701207454
#> 47 1.420995810 1.601339097 1.396442779
#> 48 3.405244971 1.876423665 4.818320993
#> 49 2.446367879 4.942733281 1.918220026
#> 50 0.373382213 -0.811619200 2.145960417
#> 51 0.858730865 2.844229971 2.215893641
#> 52 2.048278126 1.876438183 2.253066255
#> 53 -0.979401859 0.066992787 1.239294862
#> 54 -1.520667823 -0.517780882 0.002562199
#> 55 0.649664697 0.296776545 0.993825267
#> 56 4.379073801 2.422662868 0.795863984
#> 57 -0.328722937 1.480830939 -1.445882168
#> 58 0.646239216 0.424770897 -1.916304907
#> 59 0.835999391 0.217055270 -0.355409430
#> 60 0.142267982 2.659357457 -0.333557662
#> 61 1.587819101 2.699486648 -0.405668792
#> 62 1.082524348 -0.011507182 0.161447095
#> 63 -1.299067758 1.555475543 -0.651822690
#> 64 0.351846112 0.605027979 2.046577980
#> 65 -0.279595862 1.236295365 -0.684431280
#> 66 0.115635072 -0.342677375 -0.311295514
#> 67 2.599415169 -0.513369614 2.115479969
#> 68 -0.943343694 -0.906440767 0.753327404
#> 69 -0.891525122 -0.467958901 1.752160922
#> 70 -0.375173649 1.154414206 0.965969722
#> 71 -0.592328994 -0.336852088 1.329634282
#> 72 0.719152392 1.226426188 0.316414278
#> 73 1.599438191 0.789638349 0.899306546
#> 74 -0.332396124 -0.433700522 0.629458828
#> 75 0.175928921 0.707616811 2.808930860
#> 76 -0.311789389 -1.996944450 3.564422436
#> 77 2.868493105 0.326425814 -0.441878566
#> 78 -0.250515866 1.272618452 0.526962588
#> 79 0.398301132 0.929595781 2.317926260
#> 80 0.382728205 -0.729808449 2.075454233
#> 81 1.380853148 -0.655486117 1.238821897
#> 82 1.096240272 0.151342211 1.187553629
#> 83 0.794919057 3.466323051 1.677363592
#> 84 0.659773370 3.554223820 -1.116737022
#> 85 1.416964480 3.808228110 -0.272035393
#> 86 0.430344619 -0.918540236 3.601938769
#> 87 -1.503773245 -0.173989015 2.884114421
#> 88 -0.529029913 0.420256120 5.698224578
#> 89 1.230771112 -0.287094234 2.761662804
#> 90 0.560078571 2.048855290 1.138288790
#> 91 1.959411459 0.763497433 1.756392549
#> 92 0.698357920 0.787654206 1.640998942
#> 93 0.678480280 -0.093837593 1.648291943
#> 94 0.840604819 0.001959162 3.568538018
#> 95 0.992731804 2.524498697 2.340271301
#> 96 1.033125330 3.258153919 2.484460337
#> 97 0.270032796 3.015785994 2.745792037
#> 98 0.144785071 4.052392486 1.909532374
#> 99 -1.029371553 -1.760670551 -1.074155886
#> 100 -0.954367914 1.702235497 -0.555582075
#> 101 1.308843827 1.116983364 0.941671321
#> 102 1.500843440 1.095518802 0.946854714
#> 103 1.494577889 1.072951763 0.919909252
#> 104 0.798558133 -0.636985822 0.003413918
#> 105 0.285513704 -1.433753796 -0.481099535
#> 106 0.126453352 -1.694516361 -0.600543380
#> 107 0.199419762 -1.801089988 -0.706065112
#> 108 1.633109628 1.327025910 0.877534736
#> 109 3.168548867 2.024896376 2.144656353
#> 110 1.560837730 1.359395853 0.764417737
#> 111 1.135439910 1.220869473 0.851058307
#> 112 0.261217479 1.163432444 0.991981768
#> 113 1.843241992 1.593584710 0.381671289
#> 114 2.293090839 1.445486375 0.169633396
#> 115 2.296740634 1.429809245 0.178562730
#> 116 2.068841007 1.518722645 0.489558785
#> 117 1.712187338 1.434417686 1.083257103
#> 118 1.940872105 1.366000045 1.054468126
#> 119 2.145414094 1.791237720 0.690549218
#> 120 1.978714109 1.030478751 1.275088906
#> 121 1.213570447 1.419050458 1.618787592
#> 122 2.719952322 0.630368111 0.220090980
#> 123 2.766821179 0.352451641 0.593650281
#> 124 2.594464616 1.756013836 1.877177529
#> 125 2.936896160 2.325167049 1.737290454
#> 126 2.707100980 1.227585072 2.682779876
#> 127 3.296961835 1.209751107 2.342513313
#> 128 1.296722306 1.118338487 0.941344078
#> 129 1.164383097 1.118495599 0.943855518
#> 130 1.160313003 1.118077898 0.940846150
#> 131 -0.649041547 0.346875063 -0.021614045
#> 132 -0.524727502 0.907274878 0.035813489
#> 133 -0.695460246 0.768245367 0.047280182
#> 134 1.683466167 1.219494219 1.676302177
#> 135 1.810253231 1.473661832 2.372100281
#> 136 1.964019245 1.607147790 3.098631717
#> 137 1.940204635 1.624383130 3.123261340
#> 138 1.694523083 1.534142041 1.933333163
#> 139 2.150272810 0.980817437 1.834108238
#> 140 1.732274565 1.208837658 1.699781795
#> 141 2.018227402 1.159933763 1.598592939
#> 142 2.040386417 0.970299146 1.517515220
#> 143 1.937808809 0.969671787 1.265570786
#> 144 2.194970191 0.106828516 1.279967184
#> 145 2.218212435 -0.756502792 3.028091758
#> 146 1.612798864 1.224175296 1.831972593
#> 147 1.806870188 1.544144043 2.386029080
#> 148 1.861477377 1.621354858 2.555974674
#> 149 1.896798692 1.586139397 2.744450307
#> 150 1.980146158 1.911214308 2.812690102
#> 151 1.738063572 2.032954829 2.507484513
#> 152 1.667901811 2.039924690 2.405852377
#> 153 1.534247640 2.267440783 2.311944520
#> 154 -0.147891799 0.171198695 0.928999717
#> 155 -0.877011852 -0.091166271 0.725195972
#> 156 1.299761980 1.120926701 0.940209099
#> 157 0.948655082 0.985615977 0.946679770
#> 158 0.826966290 0.854360177 0.652302687
#> 159 0.621612795 0.779146856 0.439322451
#> 160 0.336050797 1.090538403 -0.928180900
#> 161 0.276575654 1.044332560 -1.180755300
#> 162 0.478283058 1.413563401 -0.385856446
#> 163 0.551283293 0.668836582 0.584137161
#> 164 0.594216305 1.017376552 0.175590443
#> 165 0.406613061 0.795359672 0.152480195
#> 166 0.119665632 0.783019034 0.132263730
#> 167 -0.226411699 0.956404490 0.461912941
#> 168 -0.002138993 0.579930789 -0.248365631
#> 169 0.388736091 0.189700133 1.174068323
#> 170 0.679411860 -0.359701226 1.522352945
#> 171 -0.855565241 -0.674511032 1.263190047
#> 172 0.048661117 0.153345062 1.444276295
#> 173 0.042746877 0.162667651 1.428068822
#> 174 0.014082113 0.037885115 1.000794444
#> 175 0.237042152 0.283856183 0.973912293
#> 176 1.156151241 1.005563482 0.609108318
#> 177 -0.064609116 -0.621932444 3.137044171
#> 178 0.972129054 0.867613889 0.725424288
#> 179 1.025171086 0.716639048 0.757475405
#> 180 1.123283232 0.595091884 0.699959101
#> 181 0.621294968 0.630106695 1.031045258
#> 182 0.405464837 0.134241374 2.121178648
#> 183 0.990603910 1.836390418 0.701632784
#> 184 0.953120717 2.926692616 0.486821499
#> 185 1.016547218 3.488081666 -0.392022456
#> 186 0.591549056 0.900698445 1.138580809
#> 187 0.563944049 1.086133686 2.126388552
#> 188 0.268872389 -0.355935806 3.459696990
#> 189 0.080471955 -0.092747344 3.547370950
#> 190 -0.936271794 0.107362828 4.236832864
#> 191 0.634698796 1.579721293 2.204867160
#> 192 0.752897750 1.473613342 2.223438386
#> 193 0.792236063 1.103061208 2.199555594
#> 194 0.795248656 1.086589529 2.171934487
#> 195 0.952624971 1.259177316 1.634498265
#> 196 1.192887579 0.950371055 1.675491901
#> 197 0.936047239 2.472161931 2.356507086
#> 198 0.261511431 3.286631493 2.312114168
#> 199 -0.967327452 -0.014804246 -0.784591384
(traits_SE = as_phylo4d(psem, what="Std. Error"))
#> label node ancestor edge.length node.type BM NL DD
#> 1 s1 1 107 0.5640308162 tip NA NA NA
#> 2 s2 2 107 0.5640308162 tip NA NA NA
#> 3 s3 3 106 0.6358275951 tip NA NA NA
#> 4 s4 4 105 0.7144448083 tip NA NA NA
#> 5 s5 5 104 1.1830950600 tip NA NA NA
#> 6 s6 6 109 0.0361022107 tip NA NA NA
#> 7 s7 7 109 0.0361022107 tip NA NA NA
#> 8 s8 8 112 0.5022074646 tip NA NA NA
#> 9 s9 9 112 0.5022074646 tip NA NA NA
#> 10 s10 10 111 1.7871837580 tip NA NA NA
#> 11 s11 11 116 0.5913975424 tip NA NA NA
#> 12 s12 12 119 0.0477228892 tip NA NA NA
#> 13 s13 13 119 0.0477228892 tip NA NA NA
#> 14 s14 14 120 0.1142573039 tip NA NA NA
#> 15 s15 15 120 0.1142573039 tip NA NA NA
#> 16 s16 16 121 0.2756963162 tip NA NA NA
#> 17 s17 17 121 0.2756963162 tip NA NA NA
#> 18 s18 18 122 0.5512595516 tip NA NA NA
#> 19 s19 19 123 0.0349638989 tip NA NA NA
#> 20 s20 20 123 0.0349638989 tip NA NA NA
#> 21 s21 21 114 0.8767527377 tip NA NA NA
#> 22 s22 22 113 1.7461743450 tip NA NA NA
#> 23 s23 23 125 0.9075157185 tip NA NA NA
#> 24 s24 24 125 0.9075157185 tip NA NA NA
#> 25 s25 25 126 0.5415591015 tip NA NA NA
#> 26 s26 26 127 0.1089356405 tip NA NA NA
#> 27 s27 27 127 0.1089356405 tip NA NA NA
#> 28 s28 28 130 3.0857795440 tip NA NA NA
#> 29 s29 29 131 1.6399242000 tip NA NA NA
#> 30 s30 30 132 0.8944032869 tip NA NA NA
#> 31 s31 31 133 0.7715950937 tip NA NA NA
#> 32 s32 32 133 0.7715950937 tip NA NA NA
#> 33 s33 33 136 0.8699913472 tip NA NA NA
#> 34 s34 34 137 0.8479589114 tip NA NA NA
#> 35 s35 35 137 0.8479589114 tip NA NA NA
#> 36 s36 36 138 0.4591954289 tip NA NA NA
#> 37 s37 37 139 0.1736071099 tip NA NA NA
#> 38 s38 38 139 0.1736071099 tip NA NA NA
#> 39 s39 39 141 2.0905969730 tip NA NA NA
#> 40 s40 40 143 0.0744131178 tip NA NA NA
#> 41 s41 41 143 0.0744131178 tip NA NA NA
#> 42 s42 42 144 0.9370864528 tip NA NA NA
#> 43 s43 43 145 0.0881684468 tip NA NA NA
#> 44 s44 44 145 0.0881684468 tip NA NA NA
#> 45 s45 45 147 1.7204295900 tip NA NA NA
#> 46 s46 46 149 1.1842473100 tip NA NA NA
#> 47 s47 47 149 1.1842473100 tip NA NA NA
#> 48 s48 48 150 1.0253154590 tip NA NA NA
#> 49 s49 49 152 0.7195368746 tip NA NA NA
#> 50 s50 50 152 0.7195368746 tip NA NA NA
#> 51 s51 51 153 0.3613256451 tip NA NA NA
#> 52 s52 52 153 0.3613256451 tip NA NA NA
#> 53 s53 53 155 0.3002640020 tip NA NA NA
#> 54 s54 54 155 0.3002640020 tip NA NA NA
#> 55 s55 55 154 0.5937157619 tip NA NA NA
#> 56 s56 56 156 3.2486997580 tip NA NA NA
#> 57 s57 57 161 0.4215356986 tip NA NA NA
#> 58 s58 58 161 0.4215356986 tip NA NA NA
#> 59 s59 59 162 0.0698869058 tip NA NA NA
#> 60 s60 60 162 0.0698869058 tip NA NA NA
#> 61 s61 61 164 0.9090035873 tip NA NA NA
#> 62 s62 62 165 0.7237639845 tip NA NA NA
#> 63 s63 63 167 0.3390345394 tip NA NA NA
#> 64 s64 64 167 0.3390345394 tip NA NA NA
#> 65 s65 65 168 0.3269574705 tip NA NA NA
#> 66 s66 66 168 0.3269574705 tip NA NA NA
#> 67 s67 67 170 0.4816150364 tip NA NA NA
#> 68 s68 68 171 0.0359279485 tip NA NA NA
#> 69 s69 69 171 0.0359279485 tip NA NA NA
#> 70 s70 70 173 0.6413136611 tip NA NA NA
#> 71 s71 71 175 0.0945133814 tip NA NA NA
#> 72 s72 72 176 0.0006422211 tip NA NA NA
#> 73 s73 73 176 0.0006422211 tip NA NA NA
#> 74 s74 74 174 0.3139612126 tip NA NA NA
#> 75 s75 75 177 0.0359670563 tip NA NA NA
#> 76 s76 76 177 0.0359670563 tip NA NA NA
#> 77 s77 77 180 0.8668137583 tip NA NA NA
#> 78 s78 78 181 0.5981367654 tip NA NA NA
#> 79 s79 79 182 0.0727809267 tip NA NA NA
#> 80 s80 80 182 0.0727809267 tip NA NA NA
#> 81 s81 81 179 1.5434906440 tip NA NA NA
#> 82 s82 82 183 0.8078943991 tip NA NA NA
#> 83 s83 83 184 0.4661635151 tip NA NA NA
#> 84 s84 84 185 0.1900157199 tip NA NA NA
#> 85 s85 85 185 0.1900157199 tip NA NA NA
#> 86 s86 86 188 0.2378751898 tip NA NA NA
#> 87 s87 87 190 0.0040209131 tip NA NA NA
#> 88 s88 88 190 0.0040209131 tip NA NA NA
#> 89 s89 89 189 0.0295310172 tip NA NA NA
#> 90 s90 90 195 0.3502461608 tip NA NA NA
#> 91 s91 91 196 0.1859710332 tip NA NA NA
#> 92 s92 92 196 0.1859710332 tip NA NA NA
#> 93 s93 93 194 0.8106943515 tip NA NA NA
#> 94 s94 94 193 0.8259283637 tip NA NA NA
#> 95 s95 95 197 0.4469879611 tip NA NA NA
#> 96 s96 96 197 0.4469879611 tip NA NA NA
#> 97 s97 97 198 0.2644025504 tip NA NA NA
#> 98 s98 98 198 0.2644025504 tip NA NA NA
#> 99 s99 99 199 0.0717127012 tip NA NA NA
#> 100 s100 100 199 0.0717127012 tip NA NA NA
#> 101 <NA> 101 0 NA root 1.22322635 1.61418789 1.72525631
#> 102 <NA> 102 101 0.3278789676 internal 1.30071498 1.71644304 1.83454740
#> 103 <NA> 103 102 0.0448143702 internal 1.31380257 1.73371363 1.85300633
#> 104 <NA> 104 103 1.7536273230 internal 1.37288352 1.81167774 1.93633497
#> 105 <NA> 105 104 0.4686502517 internal 0.97714845 1.28945978 1.37818444
#> 106 <NA> 106 105 0.0786172132 internal 0.91260141 1.20428254 1.28714636
#> 107 <NA> 107 106 0.0717967789 internal 0.91028188 1.20122166 1.28387486
#> 108 <NA> 108 103 0.5388417629 internal 1.39262282 1.83772602 1.96417557
#> 109 <NA> 109 108 2.3617784090 internal 0.30636597 0.40428514 0.43210304
#> 110 <NA> 110 108 0.1838847379 internal 1.36644386 1.80317986 1.92725237
#> 111 <NA> 111 110 0.4268121240 internal 1.51142111 1.99449403 2.13173041
#> 112 <NA> 112 111 1.2849762930 internal 1.07717612 1.42145781 1.51926493
#> 113 <NA> 113 110 0.4678215366 internal 1.44312706 1.90437217 2.03540748
#> 114 <NA> 114 113 0.8694216075 internal 0.97715330 1.28946619 1.37819129
#> 115 <NA> 115 114 0.0071530214 internal 0.97044019 1.28060746 1.36872301
#> 116 <NA> 116 115 0.2782021739 internal 0.88470104 1.16746480 1.24779527
#> 117 <NA> 117 116 0.1696001798 internal 0.74979954 0.98944675 1.05752823
#> 118 <NA> 118 117 0.1745800373 internal 0.64458322 0.85060171 0.90912959
#> 119 <NA> 119 118 0.1994944362 internal 0.34098890 0.44997408 0.48093573
#> 120 <NA> 120 118 0.1329600215 internal 0.49663196 0.65536300 0.70045697
#> 121 <NA> 121 117 0.1461010464 internal 0.70970095 0.93653205 1.00097259
#> 122 <NA> 122 115 0.3183401648 internal 0.98266488 1.29673935 1.38596490
#> 123 <NA> 123 122 0.5162956527 internal 0.29920899 0.39484068 0.42200872
#> 124 <NA> 124 102 1.5076279270 internal 1.49221553 1.96915006 2.10464258
#> 125 <NA> 125 124 0.5663931071 internal 1.32624680 1.75013522 1.87055785
#> 126 <NA> 126 124 0.9323497240 internal 1.07523634 1.41889804 1.51652903
#> 127 <NA> 127 126 0.4326234610 internal 0.51732351 0.68266788 0.72964063
#> 128 <NA> 128 101 0.0206999989 internal 1.20634454 1.59191040 1.70144596
#> 129 <NA> 129 128 0.2000464880 internal 1.25574263 1.65709685 1.77111774
#> 130 <NA> 130 129 0.0028896898 internal 1.25884677 1.66119313 1.77549587
#> 131 <NA> 131 130 1.4458553430 internal 1.57854250 2.08306843 2.22639940
#> 132 <NA> 132 131 0.7455209135 internal 1.18802246 1.56773230 1.67560422
#> 133 <NA> 133 132 0.1228081933 internal 1.13999603 1.50435591 1.60786705
#> 134 <NA> 134 129 0.6949407786 internal 1.20257065 1.58693032 1.69612321
#> 135 <NA> 135 134 0.9138552433 internal 1.38787894 1.83146592 1.95748473
#> 136 <NA> 136 135 0.6098818644 internal 1.11567674 1.47226380 1.57356677
#> 137 <NA> 137 136 0.0220324358 internal 1.11103546 1.46613910 1.56702064
#> 138 <NA> 138 135 1.0206777830 internal 0.97459019 1.28608387 1.37457624
#> 139 <NA> 139 138 0.2855883190 internal 0.63244106 0.83457873 0.89200411
#> 140 <NA> 140 134 0.0802496379 internal 1.16877200 1.54232911 1.64845310
#> 141 <NA> 141 140 0.2228818440 internal 1.28533627 1.69614907 1.81285704
#> 142 <NA> 142 141 0.2076500851 internal 1.37909625 1.81987615 1.94509749
#> 143 <NA> 143 142 1.8085337700 internal 0.43767253 0.57755925 0.61729973
#> 144 <NA> 144 142 0.9458604351 internal 1.34725029 1.77785174 1.90018148
#> 145 <NA> 145 144 0.8489180060 internal 0.47300751 0.62418782 0.66713669
#> 146 <NA> 146 140 0.1770607381 internal 1.23211080 1.62591193 1.73778706
#> 147 <NA> 147 146 0.4159884892 internal 1.24623965 1.64455658 1.75771460
#> 148 <NA> 148 147 0.1695261804 internal 1.21017992 1.59697162 1.70685543
#> 149 <NA> 149 148 0.3666560998 internal 1.32044920 1.74248462 1.86238084
#> 150 <NA> 150 148 0.5255879506 internal 1.12365874 1.48279697 1.58482469
#> 151 <NA> 151 150 0.2079515725 internal 1.00451302 1.32557048 1.41677983
#> 152 <NA> 152 151 0.0978270115 internal 1.01302888 1.33680815 1.42879073
#> 153 <NA> 153 151 0.4560382411 internal 0.87087189 1.14921565 1.22829044
#> 154 <NA> 154 146 1.5427023170 internal 1.08223037 1.42812747 1.52639352
#> 155 <NA> 155 154 0.2934517599 internal 0.80865458 1.06711274 1.14053822
#> 156 <NA> 156 128 0.0400159638 internal 1.23140386 1.62497905 1.73678999
#> 157 <NA> 157 156 0.4026925133 internal 1.35918408 1.79359975 1.91701308
#> 158 <NA> 158 157 0.7951233038 internal 1.27358140 1.68063717 1.79627781
#> 159 <NA> 159 158 0.3736798197 internal 1.22652022 1.61853452 1.72990203
#> 160 <NA> 160 159 1.1492712710 internal 0.94650940 1.24902804 1.33497069
#> 161 <NA> 161 160 0.1063971509 internal 0.87500944 1.15467562 1.23412609
#> 162 <NA> 162 160 0.4580459438 internal 0.41761870 0.55109591 0.58901551
#> 163 <NA> 163 159 0.2335971502 internal 1.16536491 1.53783306 1.64364769
#> 164 <NA> 164 163 0.5346033834 internal 1.07091058 1.41318971 1.51042792
#> 165 <NA> 165 164 0.1852396028 internal 0.95150270 1.25561727 1.34201330
#> 166 <NA> 166 165 0.1474062575 internal 0.86886630 1.14656904 1.22546172
#> 167 <NA> 167 166 0.2373231876 internal 0.80532548 1.06271962 1.13584282
#> 168 <NA> 168 166 0.2494002564 internal 0.79695072 1.05166816 1.12403094
#> 169 <NA> 169 163 0.4262080943 internal 1.10440718 1.45739233 1.55767202
#> 170 <NA> 170 169 0.5357838400 internal 0.98598517 1.30112086 1.39064788
#> 171 <NA> 171 170 0.4456870879 internal 0.30302820 0.39988057 0.42739540
#> 172 <NA> 172 169 0.3680846598 internal 0.89979805 1.18738704 1.26908831
#> 173 <NA> 173 172 0.0080005555 internal 0.89702741 1.18373086 1.26518056
#> 174 <NA> 174 173 0.3273524485 internal 0.77398260 1.02135908 1.09163636
#> 175 <NA> 175 174 0.2194478311 internal 0.47112032 0.62169745 0.66447497
#> 176 <NA> 176 175 0.0938711603 internal 0.04095469 0.05404443 0.05776309
#> 177 <NA> 177 172 0.6133471602 internal 0.30345934 0.40044951 0.42800348
#> 178 <NA> 178 158 0.3661103260 internal 1.25575706 1.65711591 1.77113810
#> 179 <NA> 179 178 0.1412829703 internal 1.28149047 1.69107409 1.80743287
#> 180 <NA> 180 179 0.6766768859 internal 1.16906592 1.54271697 1.64886765
#> 181 <NA> 181 180 0.2686769929 internal 1.04754240 1.38235271 1.47746911
#> 182 <NA> 182 181 0.5253558386 internal 0.42744225 0.56405922 0.60287079
#> 183 <NA> 183 178 0.8768792154 internal 1.16688879 1.53984400 1.64579700
#> 184 <NA> 184 183 0.3417308840 internal 0.93124907 1.22889027 1.31344729
#> 185 <NA> 185 184 0.2761477952 internal 0.65326012 0.86205188 0.92136761
#> 186 <NA> 186 157 0.4967710625 internal 1.52763597 2.01589140 2.15460008
#> 187 <NA> 187 186 0.8026320886 internal 1.36167014 1.79688039 1.92051945
#> 188 <NA> 188 187 1.3087289040 internal 0.75183416 0.99213166 1.06039788
#> 189 <NA> 189 188 0.2083441725 internal 0.26849975 0.35431631 0.37869597
#> 190 <NA> 190 189 0.0255101041 internal 0.10068396 0.13286406 0.14200612
#> 191 <NA> 191 187 0.3703056422 internal 1.13842365 1.50228097 1.60564934
#> 192 <NA> 192 191 0.1968950188 internal 1.00764393 1.32970209 1.42119572
#> 193 <NA> 193 192 0.1534750686 internal 0.94424288 1.24603711 1.33177395
#> 194 <NA> 194 193 0.0152340122 internal 0.94588044 1.24819805 1.33408359
#> 195 <NA> 195 194 0.4604481907 internal 0.80011381 1.05584222 1.12849221
#> 196 <NA> 196 195 0.1642751276 internal 0.62798360 0.82869660 0.88571724
#> 197 <NA> 197 192 0.5324154713 internal 0.95527123 1.26059028 1.34732849
#> 198 <NA> 198 191 0.9118959007 internal 0.79057873 1.04325957 1.11504378
#> 199 <NA> 199 186 2.2775234810 internal 0.43045988 0.56804132 0.60712690
#> RS LS
#> 1 NA NA
#> 2 NA NA
#> 3 NA NA
#> 4 NA NA
#> 5 NA NA
#> 6 NA NA
#> 7 NA NA
#> 8 NA NA
#> 9 NA NA
#> 10 NA NA
#> 11 NA NA
#> 12 NA NA
#> 13 NA NA
#> 14 NA NA
#> 15 NA NA
#> 16 NA NA
#> 17 NA NA
#> 18 NA NA
#> 19 NA NA
#> 20 NA NA
#> 21 NA NA
#> 22 NA NA
#> 23 NA NA
#> 24 NA NA
#> 25 NA NA
#> 26 NA NA
#> 27 NA NA
#> 28 NA NA
#> 29 NA NA
#> 30 NA NA
#> 31 NA NA
#> 32 NA NA
#> 33 NA NA
#> 34 NA NA
#> 35 NA NA
#> 36 NA NA
#> 37 NA NA
#> 38 NA NA
#> 39 NA NA
#> 40 NA NA
#> 41 NA NA
#> 42 NA NA
#> 43 NA NA
#> 44 NA NA
#> 45 NA NA
#> 46 NA NA
#> 47 NA NA
#> 48 NA NA
#> 49 NA NA
#> 50 NA NA
#> 51 NA NA
#> 52 NA NA
#> 53 NA NA
#> 54 NA NA
#> 55 NA NA
#> 56 NA NA
#> 57 NA NA
#> 58 NA NA
#> 59 NA NA
#> 60 NA NA
#> 61 NA NA
#> 62 NA NA
#> 63 NA NA
#> 64 NA NA
#> 65 NA NA
#> 66 NA NA
#> 67 NA NA
#> 68 NA NA
#> 69 NA NA
#> 70 NA NA
#> 71 NA NA
#> 72 NA NA
#> 73 NA NA
#> 74 NA NA
#> 75 NA NA
#> 76 NA NA
#> 77 NA NA
#> 78 NA NA
#> 79 NA NA
#> 80 NA NA
#> 81 NA NA
#> 82 NA NA
#> 83 NA NA
#> 84 NA NA
#> 85 NA NA
#> 86 NA NA
#> 87 NA NA
#> 88 NA NA
#> 89 NA NA
#> 90 NA NA
#> 91 NA NA
#> 92 NA NA
#> 93 NA NA
#> 94 NA NA
#> 95 NA NA
#> 96 NA NA
#> 97 NA NA
#> 98 NA NA
#> 99 NA NA
#> 100 NA NA
#> 101 1.34657639 2.14730314
#> 102 1.43187897 2.28332994
#> 103 1.44628631 2.30630446
#> 104 1.51132499 2.41001765
#> 105 1.07568402 1.71532760
#> 106 1.00462806 1.60201901
#> 107 1.00207463 1.59794722
#> 108 1.53305479 2.44466885
#> 109 0.33725989 0.53780774
#> 110 1.50423594 2.39871319
#> 111 1.66383269 2.65321238
#> 112 1.18579847 1.89092040
#> 113 1.58865188 2.53332612
#> 114 1.07568936 1.71533613
#> 115 1.06829930 1.70355164
#> 116 0.97391422 1.55304153
#> 117 0.82540927 1.31622975
#> 118 0.70958294 1.13152858
#> 119 0.37537419 0.59858630
#> 120 0.54671228 0.87180869
#> 121 0.78126714 1.24583899
#> 122 1.08175673 1.72501138
#> 123 0.32938120 0.52524408
#> 124 1.64269043 2.61949810
#> 125 1.45998542 2.32814958
#> 126 1.18366308 1.88751522
#> 127 0.56949037 0.90813151
#> 128 1.32799223 2.11766810
#> 129 1.38237161 2.20438358
#> 130 1.38578878 2.20983273
#> 131 1.73772260 2.77104010
#> 132 1.30782254 2.08550473
#> 133 1.25495314 2.00119713
#> 134 1.32383778 2.11104325
#> 135 1.52783254 2.43634124
#> 136 1.22818149 1.95850601
#> 137 1.22307219 1.95035852
#> 138 1.07286779 1.71083674
#> 139 0.69621637 1.11021372
#> 140 1.28663087 2.05171168
#> 141 1.41494947 2.25633350
#> 142 1.51816420 2.42092373
#> 143 0.48180739 0.76830882
#> 144 1.48310690 2.36501999
#> 145 0.52070554 0.83033733
#> 146 1.35635675 2.16289927
#> 147 1.37191036 2.18770166
#> 148 1.33221436 2.12440088
#> 149 1.45360319 2.31797223
#> 150 1.23696839 1.97251795
#> 151 1.10580803 1.76336452
#> 152 1.11518263 1.77831364
#> 153 0.95869054 1.52876526
#> 154 1.19136239 1.89979285
#> 155 0.89019924 1.41954636
#> 156 1.35557853 2.16165828
#> 157 1.49624409 2.38596907
#> 158 1.40200925 2.23569852
#> 159 1.35020242 2.15308533
#> 160 1.04195534 1.66154254
#> 161 0.96324532 1.53602848
#> 162 0.45973133 0.73310547
#> 163 1.28288021 2.04573073
#> 164 1.17890112 1.87992161
#> 165 1.04745215 1.67030797
#> 166 0.95648271 1.52524456
#> 167 0.88653444 1.41370232
#> 168 0.87731517 1.39900092
#> 169 1.21577551 1.93872296
#> 170 1.08541183 1.73083996
#> 171 0.33358554 0.53194849
#> 172 0.99053361 1.57954346
#> 173 0.98748358 1.57467976
#> 174 0.85203094 1.35868171
#> 175 0.51862805 0.82702448
#> 176 0.04508456 0.07189359
#> 177 0.33406015 0.53270532
#> 178 1.38238750 2.20440892
#> 179 1.41071586 2.24958242
#> 180 1.28695443 2.05222763
#> 181 1.15317650 1.83890013
#> 182 0.47054549 0.75035015
#> 183 1.28455776 2.04840581
#> 184 1.02515615 1.63475390
#> 185 0.71913482 1.14676037
#> 186 1.68168266 2.68167663
#> 187 1.49898084 2.39033320
#> 188 0.82764906 1.31980140
#> 189 0.29557524 0.47133579
#> 190 0.11083692 0.17674487
#> 191 1.25322220 1.99843690
#> 192 1.10925466 1.76886067
#> 193 1.03946026 1.65756379
#> 194 1.04126295 1.66043843
#> 195 0.88079722 1.40455354
#> 196 0.69130942 1.10238891
#> 197 1.05160070 1.67692341
#> 198 0.87030062 1.38781525
#> 199 0.47386741 0.75564742
# Convert to sem and plot
library(sem)
my_sem = as_sem(psem)
pathDiagram( model = my_sem,
style = "traditional",
edge.labels = "values" )
#> Loading required namespace: DiagrammeR
effects( my_sem )
#>
#> Total Effects (column on row)
#> BM NL DD
#> DD 0.6296696 0.6750692 0.0000000
#> RS -0.1387108 -0.1487120 -0.2202914
#> LS 1.3366815 0.0000000 0.0000000
#> NL 0.9327482 0.0000000 0.0000000
#>
#> Direct Effects
#> BM NL DD
#> DD 0.0000000 0.6750692 0.0000000
#> RS 0.0000000 0.0000000 -0.2202914
#> LS 1.3366815 0.0000000 0.0000000
#> NL 0.9327482 0.0000000 0.0000000
#>
#> Indirect Effects
#> BM NL DD
#> DD 0.6296696 0.000000 0
#> RS -0.1387108 -0.148712 0
#> LS 0.0000000 0.000000 0
#> NL 0.0000000 0.000000 0
# Plot using semPlot
if( require(semPlot) ){
myplot = semPlotModel( my_sem )
semPaths( my_sem,
nodeLabels = myplot@Vars$name )
}
#> Loading required package: semPlot
