dsem model description

James T. Thorson

Dynamic structural equation models

dsem involves specifying a dynamic structural equation model (DSEM). This DSEM be viewed either:

1. Weak interpretation: as an expressive interface to parameterize the correlation among variables, using as many or few parameters as might be appropriate; or
2. Strong interpretation: as a structural causal model, allowing predictions about the consequence of counterfactual changes to the system.

We introduce DSEM first from the perspective of a software user (i.e., the interface) and then from the perspective of a statistician (i.e., the equations and their interpretation).

Viewpoint 1: Software interface

To specify a DSEM, the user uses arrow-and-lag notation, based on arrow notation derived from package sem. For example, to specify a first-order autoregressive process with variable $x$ this involves:

x -> x, 1, ar1
x <-> x, 0, sd

This then estimates a single parameter representing first-order autoregression (represented with a one-headed arrow), as well as the Cholesky decomposition of the exogenous covariance of of model variables (specified with two-headed arrows). See ?make_dsem_ram Details section for more details about syntax.

If there were four time-intervals ($T=4$) this would then result in the path matrix:

$$\mathbf P_{\mathrm{joint}} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ \rho & 0 & 0 & 0 \\ 0 & \rho & 0 & 0 \\ 0 & 0 & \rho & 0 \end{pmatrix}$$ This joint path matrix then represents the partial effect of each variable and time (column) on each other variable and time (row).

DSEM interactions can be as complicated or simple as desired, and can include:

1. Latent variables and loops (i.e., they are not restricted to directed acyclic graphs);
2. Values that are fixed a priori, where the parameter_name is provided as NA and the starting value that follows is the fixed value;
3. Values that are mirrored among path coefficients, where the same parameter_name is provided for multiple rows of the text file.

The user also specifies a distribution for measurement errors for each variable using arguement family, and whether each time-series starts from its stationary distribution or from some non-equilibrium initial condition using argument estimate_delta0. If the latter is specified, then variables will tend to converge back on the stationary distribution at a rate that is determined by estimated parameters.

Viewpoint 2: Mathematical details

The DSEM defines a generalized linear mixed model (GLMM) for a $T \times J$ matrix $\mathbf{Y}$, where $y_{tj}$ is the measurement in time $t$ for variable $j$. This measurement matrix can include missing values $y_{tj} = \mathrm{NA}$, and it will estimate a $T \times J$ matrix of latent states $\mathbf{X}$ for all modeled times and variables.

DSEM includes multiple distribution for measurement errors. For example, if the user specifies family[j] = "fixed" then:

$$y_{tj} = x_{tj} + d_{tj}$$ for all years. Alternatively, if the user specifies family[j] = "normal" then: $$y_{tj} \sim \mathrm{Normal}( x_{tj} + d_{tj}, {\sigma_j}^2)$$ and ${\sigma_j}^2$ is then included as an estimated parameter. These expressions include the $T \times J$ matrix $\mathbf D$ representing the ongoing impact of initial conditions $d_{tj}$ for each variable and year, as explained in detail below.

The specified DSEM then results in Gaussian Markov random field for latent states:

$$\mathrm{vec}(\mathbf X) \sim \mathrm{GMRF}(\mathbf{0, Q}_{\mathrm{joint}})$$ where $\mathbf Q_{\mathrm{joint}}$ is a $TJ \times TJ$ precision matrix such that $\mathbf{Q_{\mathrm{joint}}}^{-1}$ is the estimated covariance among latent states. This joint precision is itself constructed from a joint path matrix $\mathbf P_{\mathrm{joint}}$ and a joint matrix of exogenous covariance $\mathbf G_{\mathrm{joint}}$:

$$\mathbf Q_{\mathrm{joint}} = ({\mathbf{I - P}_{\mathrm{joint}}}^T) \mathbf G_{\mathrm{joint}}^{-1} \mathbf G_{\mathrm{joint}}^{-T} (\mathbf{I - P_{\mathrm{joint}}})$$

Constructing the joint path matrix

The joint path matrix is itself constructed by summing across lagged and simultaneous effects. Say we specify a model with $K=2$ one-headed arrows. For each one-headed arrow, we define a $J \times J$ path matrix $\mathbf P_k$ and a lag matrix $\mathbf L_k$. For example, in a model with $J=3$ variables $(A,B,C)$ and $T=4$ times, and specifying $K=2$ one-headed arrows:

A -> B, 0, b_AB
B -> C, 1, b_BC

this then results two path matrices:

$$\mathbf P_1 = \begin{pmatrix} 0 & 0 & 0 \\ b_{AB} & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$$ and $$\mathbf P_2 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & b_{BC} & 0 \\ \end{pmatrix}$$ with corresponding lag matrices

$$\mathbf L_{1} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$ and $$\mathbf L_{2} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}$$ We then sum across the Kronecker product of these components to obtain the joint path matrix:

$$\mathbf P_{\mathrm{joint}} = \sum_{k=1}^{K}(\mathbf L_k \otimes \mathbf P_k)$$ where $\otimes$ is the Kronecker product. Similarly, the exogenous covariance is similar constructed from a Kronecker product, although we assume that all covariance is simultaneous (i.e., no lags are allowed for two-headed arrows):

$$\mathbf G_{\mathrm{joint}} = \mathbf I \otimes \mathbf G$$

These matrices are define a simultaneous equation model:

$$ \mathrm{vec}(\mathbf X) = \mathbf P_{\mathrm{joint}} \mathrm{vec}(\mathbf X) + \mathbf\epsilon \\ \mathbf\epsilon \sim \mathrm{MVN}( \mathbf 0, \mathbf{G_{\mathrm{joint}}}^T \mathbf G_{\mathrm{joint}} ) $$ and the precision matrix can be derived from this simultaneous equation.

Initial conditions and total effects

Imagine we have some exogenous intervention that caused a $T \times J$ matrix of changes $\mathbf C$. The total effect of this exogenous intervention would then be $(\mathbf{I - P}_{\mathrm{joint}})^{-1} \mathrm{vec}(\mathbf C)$, and we can calculate any total effect using this matrix inverse $(\mathbf{I - P}_{\mathrm{joint}})^{-1}$ (called the “Leontief matrix”). To see this, consider that the first-order effect of change $\mathbf C$ is $\mathbf P_{\mathrm{joint}} \mathrm{vec}(\mathbf C)$, but this response then in turn causes a second-order effect $\mathbf{P_{\mathrm{joint}}}^2 \mathrm{vec}(\mathbf C)$, and so on. The total effect is therefore:

$$\sum_{l=1}^{\infty} \mathbf{P_{\mathrm{joint}}}^l = (\mathbf{I - P}_{\mathrm{joint}})^{-1}$$ where this power-series of direct and indirect effects then results in the Leontief matrix (as long as the $\mathbf{I - P}$ is invertible).

We can use this expression to calculate the matrix $\mathbf D$ represents the ongoing effect of initial conditions. It is constructed from a $J$ length vector of estimated initial conditions $\mathbf\delta_1$ in time $t=1$, and we construct a $T \times J$ matrix $\mathbf\Delta$ where the first row (corresponding to year $t=1$) is $\mathbf\delta_1$ and all other elements are $0$. The ongoing effect of initial conditions can then be calculated as:

$$\mathrm{vec}(\mathbf D) = (\mathbf{I - P}_{\mathrm{joint}})^{-1} \mathrm{vec}(\mathbf\Delta)$$ Calculating the effect of initial conditions is in a sense the total effect of $\mathbf\delta_1$ in year $t=1$ on subsequent years. Calculating the effect $\mathbf D$ of initial conditions involves inverting $\mathbf{I - P}_{\mathrm{joint}}$, but this is computationally efficient using a sparse LU decomposition.

Constant conditional vs. marginal variance

We have defined the joint precision for a GMRF based on a path matrix and matrix of exogenous covariances. The exogenous (or conditional) variances are stationary for each variable over time, and some path matrices will result in a nonstationary marginal variance. To see this, consider a first-order autoregressive process

dsem = " 
x -> x, 1, ar1, 0.8
x <-> x, 0, sd, 1
"

We can parse this DSEM and construct the precision using internal functions:

# Load package
library(dsem)

# call dsem without estimating parameters
out = dsem(
  tsdata = ts(data.frame( x = rep(1,10) )),
  sem = dsem,
  control = dsem_control(
    run_model = FALSE, 
    quiet = TRUE
  )
)

# Extract covariance
Sigma1 = solve(as.matrix(out$obj$report()$Q_kk))
plot( x=1:10, y = diag(Sigma1), xlab="time", 
      ylab="Marginal variance", type="l", 
      ylim = c(0,max(diag(Sigma1))))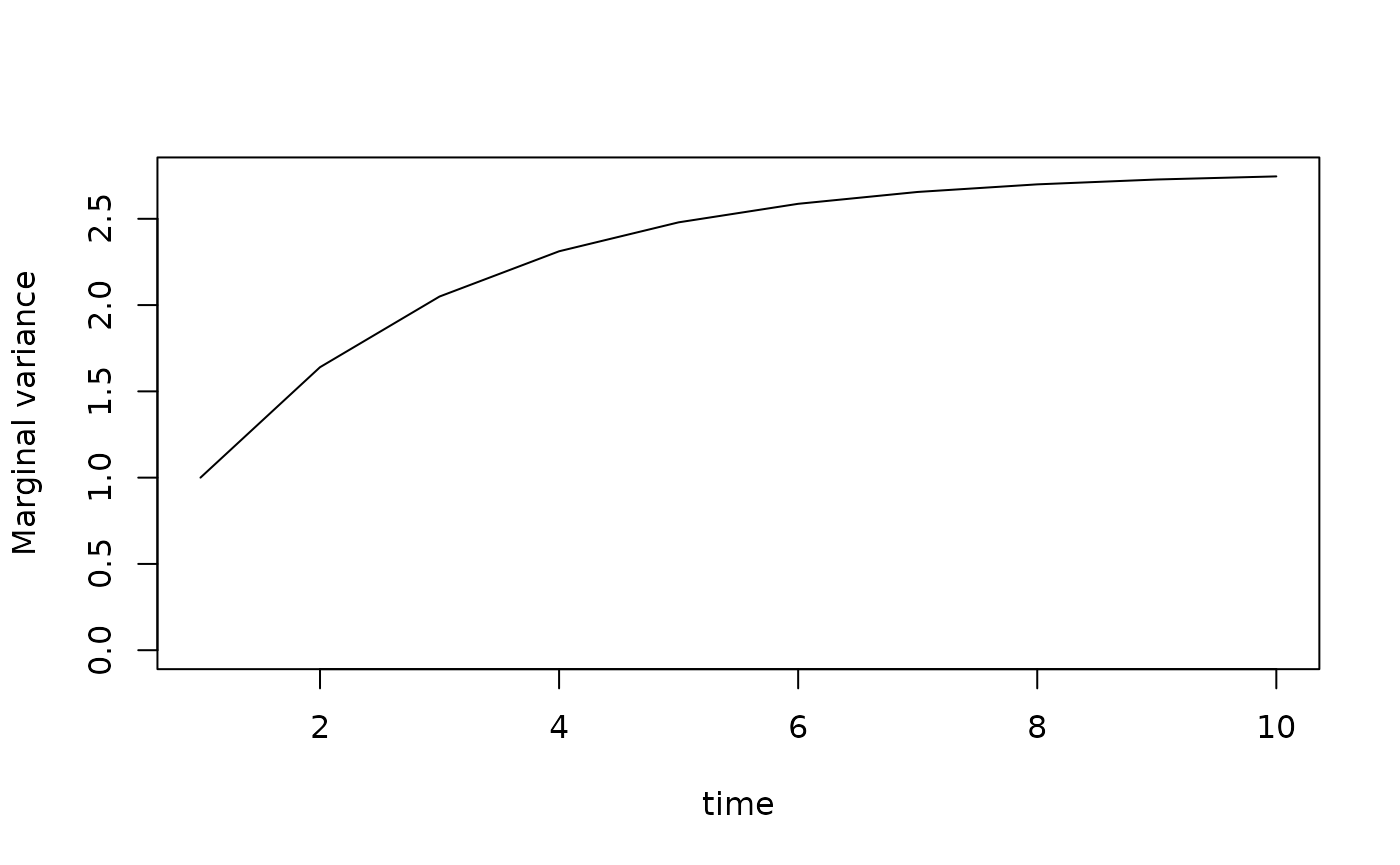

where we can see that the diagonal of this covariance matrix is non-constant.

We therefore derive an alternative specification that preserves a stationary marginal variance by rescaling the exogenous (conditional) variance.

Specifically, we see that the marginal variance is:

$$ \mathrm{Var}(\mathbf X) = \mathrm{diag}(\mathbf\Sigma) = \mathbf{ L L}^T \\ \mathbf L = (\mathbf{I - P}_{\mathrm{joint}})^{-1} \mathbf G $$ Given the properties of the Hadamard (elementwise) product, this can be rewritten as:

$$\mathrm{diag}(\mathbf\Sigma) = \mathbf{(L \circ L) 1}$$ Now suppose we have a desired vector of length $TJ$ for the constant marginal variance $\mathbf v$. We can solve for the exogenous covariance that would result in that marginal variance:

$$\mathbf u = \mathbf{(L \circ L)}^{-1} \mathbf v$$

and we can then rescale the exogenous covariance:

$$\mathrm{diag}(\mathbf G^*) = \mathbf u$$ and then using this rescaled exogenous covariance when constructing the precision of the GMRF. We can see this again using our first-order autoregressive example

# call dsem without estimating parameters
out = dsem(
  tsdata = ts(data.frame( x = rep(1,10) )),
  sem = dsem,
  control = dsem_control(
    run_model = FALSE, 
    quiet = TRUE, 
    constant_variance = "marginal"
  )
)

# Extract covariance
Sigma2 = solve(as.matrix(out$obj$report()$Q_kk))
plot( x=1:10, y = diag(Sigma2), xlab="time", 
      ylab="Marginal variance", type="l", 
      ylim = c(0,max(diag(Sigma1))))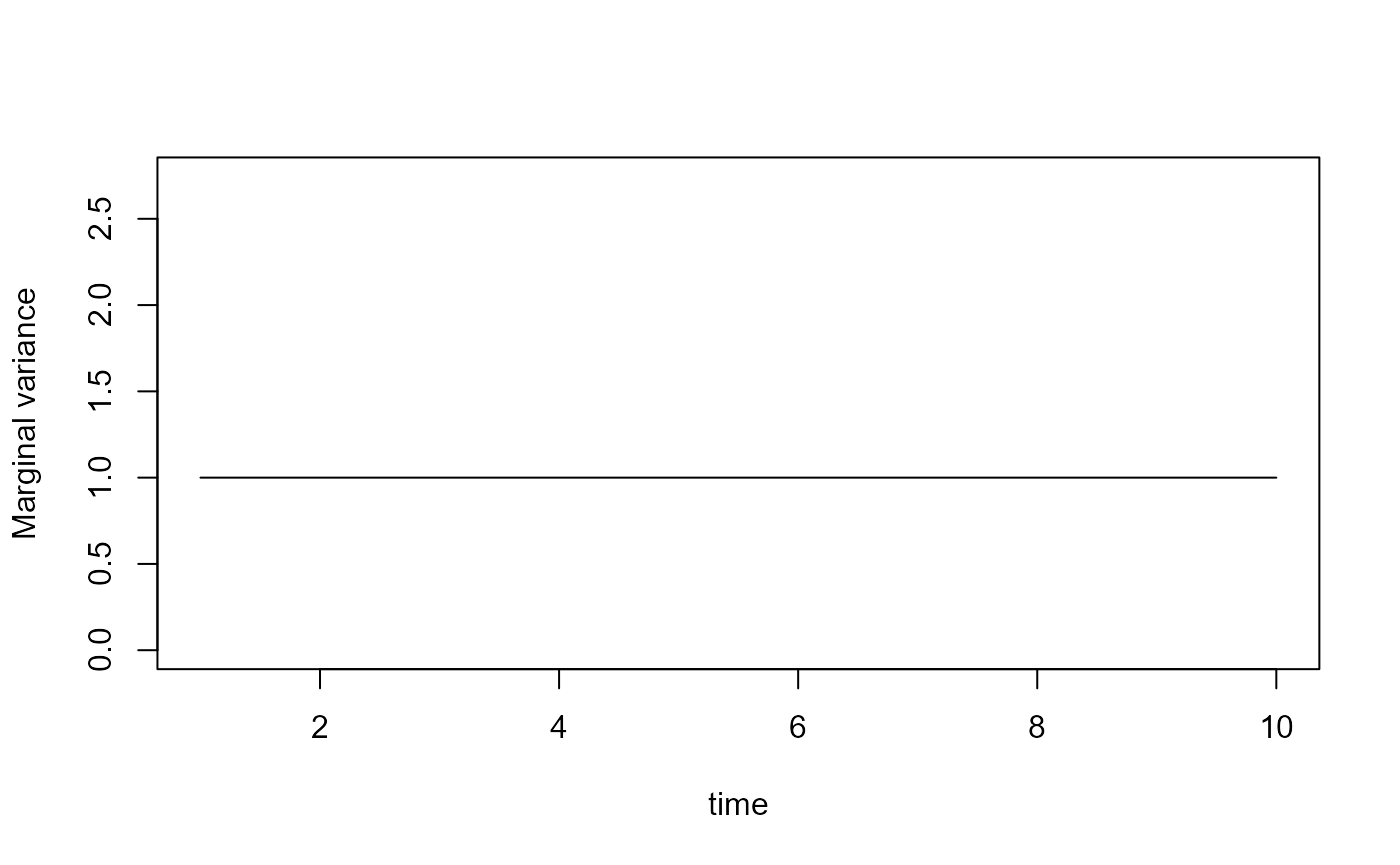

This shows that the corrected (nonstationary) exogenous variance results in a stationary marginal variance for the AR1 process. This correction can be done in two different ways that are identical when the exogenous covariance is diagonal (as it is in this simple example), but differ when specifying some exogenous covariance. However, we do not discuss this in detail here. Note that this calculating this correction for a constant marginal variance requires the inverse of the squared values of Leontief matrix (which is itself a matrix inverse). It therefore is computationally expensive for large models containing complicated dependencies.

Reduced rank models

We note that some DSEM specifications will be reduced rank. This arises for example when specifying a dynamic factor analysis, where $J$ variables are explained by $F < J$ factors that each follow a random walk:

#
dsem = "
  # Factor follows random walk with unit variance
  F <-> F, 0, NA, 1
  F -> F, 1, NA, 1
  # Loadings on two manifest variables
  F -> x, 0, b_x, 1
  F -> y, 0, b_y, 1
  # No residual variance for manifest variables
  x <-> x, 0, NA, 0
  y <-> y, 0, NA, 0
"
data = data.frame( 
  x = rnorm(10),
  y = rnorm(10),
  F = rep(NA,10)
)

# call dsem without estimating parameters
out = dsem(
  tsdata = ts(data),
  sem = dsem,
  family = c("normal","normal","fixed"),
  control = dsem_control(
    run_model = FALSE, 
    quiet = TRUE,
    gmrf_parameterization = "projection"
  )
)

We can extract the covariance and inspect the eigenvalues:

# Extract covariance
library(Matrix)
IminusRho_kk = out$obj$report()$IminusRho_kk
G_kk = out$obj$report()$Gamma_kk
Q_kk = t(IminusRho_kk) %*% t(G_kk) %*% G_kk %*% IminusRho_kk

# Display eigenvalues
eigen(Q_kk)$values
#>  [1] 3.91114561 3.65247755 3.24697960 2.73068205 2.14946019 1.55495813
#>  [7] 1.00000000 0.53389626 0.19806226 0.02233835 0.00000000 0.00000000
#> [13] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [19] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [25] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000

where this shows that the precision has a rank of 10 while being a $30 \times 30$ matrix. We therefore cannot evaluate the probability density of state matrix $\mathbf X$ using this precision matrix (i.e., the log-determinant is not defined).

To address this circumstance, we can switch to using gmrf_parameterization = "projection". This evaluates the probability density of a set of innovations $\mathbf X^*$ that follow a unit variance:

$$\mathrm{vec}(\mathbf X)^* \sim \mathrm{GMRF}(\mathbf{0, I})$$ and then projects these full-rank innovations to the reduced rank states:

$$\mathrm{vec}(\mathbf X) = (\mathbf{I - P}_{\mathrm{joint}})^{-1} \mathbf G_{\mathrm{joint}} \mathrm{vec}(\mathbf X)^*$$

This parameterization allows us to fit DSEM using a rank-deficient structural model.